|
Math and Aesthetics in Carpets, Faces, Art,
and Music

Asymmetry and Symmetry-Breaking
Article # 1 Symmetry Holds Key to Beauty
Abcnews.com
W A S H I N G T O N, Sept. 24,1998 — The same trait that
makes people love harmonious music may help them choose
a beautiful face,
researchers said today. This could be because humans learn
symmetrical patterns much faster than asymmetrical ones, said
Michael Ryan, a zoologist at the University of Texas and expert on the subject. "In
humans, the perceptual system is biased toward
processing
symmetrical signals," he said.
Recent studies indicate the
perception of beauty might not be subjective at all but instead
arises from a bias hard-wired into the sensory
system. Such studies have shown how
symmetrical body features, chiefly in the face, are viewed
as beautiful, while asymmetrical ones are not. Ryan said
another example is research
that suggests harmonic rather than discordant music strikes humans
as more pleasing because of the way the
inner ear works.
Senses Stimulated
Writing in the journal Science,
Ryan said a number of studies have indicated that physical traits
physically stimulate the senses. He says this
means the traditional theories about
genetic fitness do not tell the whole story about why animals and
humans choose "attractive" mates.
The genetic fitness theory holds that
pretty traits, such as the elaborate tail on a peacock, signal
that the animal is stronger and more fit in
other, invisible ways. But Ryan says
his studies show this is not necessarily true. "Mate choice
is important but it doesn’t explain all the
factors we find pleasing or beautiful," he
said.
"In a lot of cases females will
prefer more elaborate males but don’t get a reproductive
advantage."
Preprogrammed
Response
Water mites, which feed by sensing
their prey’s waterborne vibrations, are an example. Their choice
of mates is wholly unrelated to the male’s
reproductive ability, Ryan said. The
vibrations the males make mimic the vibrations made by copepods,
the prey that mites prefer.
He said the females are simply
already programmed to respond to the vibrations. "Any sensory
system is going to be more responsive to
some stimuli than to others," Ryan
said. "If males have a variety of options by which to signal
their sexual interest, females will favor those
who use signals they are already
keyed into." But he pointed out his "preferred preferences" theory
cannot by itself explain natural selection.
Rather, it is a helpful part in a
complex puzzle that includes the more traditional theories. "The
bottom line is the answer isn’t simply going to
be hypothesis A, hypothesis B
or hypothesis C," Ryan said.
Copyright (c)1998
ABCNEWS and Starwave Corporation
SYMMETRY BREAKING
article # 2  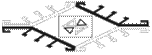
(Taken from Mathematics
and the Arts URL:
http://forum.swarthmore.edu/geometry/rugs/symmetry/
Symmetry breaking exists where symmetry is expected, but that
expectation is not met. As we often see in Oriental
carpets, it is playfulness with
symmetry that results in intriguing patterns.
In nature, symmetry is imperfect, although mathematicians may
treat it as an
 ideal. ideal.
In art, too, it seems that the approximation of symmetry,
rather than its precision,
teases the mind as it pleases the
eye.
IN
CARPETS, BORDER PATTERNS
result when any or several of the basic symmetries are
repeated in one direction. The constraints of symmetry are such
that there are seven (7) possible combinations:
GRIDS
and
Tessellations
THE EASIEST WAY TO ANALYZE
a pattern is to locate points of rotation, and lines of symmetry.
Why? Because the rigid motions
require centers of rotation and axes
of repetition or reflection for symmetry to be present.
 WHAT
IS AN AXIS? An axis is a
visible or implied line that is vertical, horizontal or diagonal, along which
designs WHAT
IS AN AXIS? An axis is a
visible or implied line that is vertical, horizontal or diagonal, along which
designs
are repeated or reflected to form patterns.
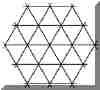
WHAT IS A GRID?
A grid is a visible or implied
series of points, or axes that intersect. Grids underlie the
structure of all two-dimensional patterns.
Grids are usually based on regular
polygons: squares, equilateral triangles, and hexagons. Or they
can be based on
rectangles, parallelograms and rhomboids.
THE ARRANGEMENT OF POLYGONS
that forms a grid is called tessellation. Other shapes may also
tessel
WHAT IS A TESSELLATION?
A tessellation is a pattern formed by the
repetition of a single unit or shape
that, when repeated, fills the plane with
no gaps and no overlaps. Familiar
examples of tessellations are the patterns
formed by paving stones or bricks,
and cross-sections of beehives.
Tessellations are not typical of
Oriental carpets except as visible grid structures.
Although they often appear in minor
borders, only rarely are tessellations used as
field patterns.
 
Conceptions of beauty are chiefly mathematical
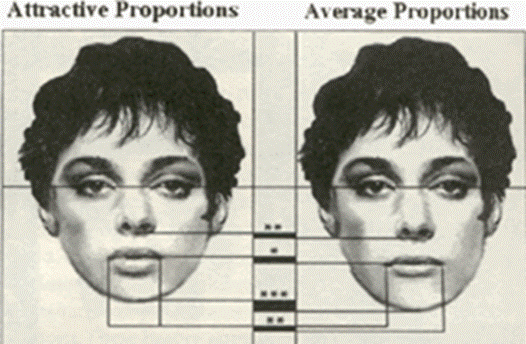
Jaw length is
important to conceptions of beauty.
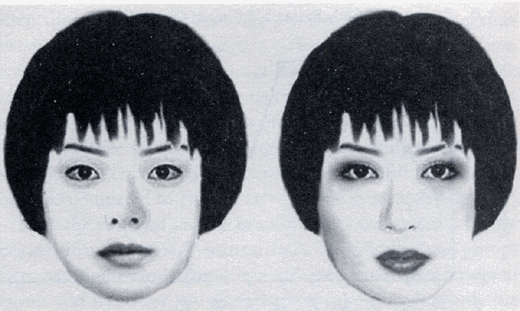
Childlike proportions are highly desirable
Visit
this fascinating website which shows the relationship between PHI,
the golden number, and beauty

This is a computer composite
of the most desirable features.

Synopsis of Article # 4
 Emblems of Mind : The Inner Life of Music and Mathematics
Emblems of Mind : The Inner Life of Music and Mathematics
by Edward Rothstein
From Kepler and the
music of the spheres to Einstein and his violin, music and
mathematics seem to share a strong relationship. This
pathbreaking book (Emblems of
Mind) seeks to unravel the mystery at the heart of that
relationship. In this elegant exploration, music
critic Edward
Rothstein reveals the profound and
intriguing parallels between music and mathematics. Invoking the
poetry of Wordsworth,
the theories of Levi-Strauss, the images of Plato and the
philosophy of Kant, Emblems of the Mind is "a harmonious virtuoso
performance".
Math and a Music Education
In the introduction
to his recent book, Emblems of Mind, Edward Rothstein,
chief music critic for the New York Times, describes how
his
education and interests
encompassed both music and mathematics "Before setting out
to make my way in the music business," he writes,
"I was in
training to become a 'pure' mathematician. Such esoteric subjects
as algebraic topology,
measure theory, and nonstandard
analysis were my preoccupations. I
would stay up nights trying to solve knotty mathematical problems, playing
with abstract phrases
and structures. "But at the same
time, I would be lured away from these constructions by another
activity. With an enthusiasm that could
come only when critical faculties are in
happy slumber, I would listen to or play a musical composition
again and again, imprinting my ear
and mind and hands with its
logic and sense. Music and
math together satisfied a sort of abstract 'appetite,' a desire
that was partly
intellectual, partly aesthetic, partly emotional,
partly, even, physical."
Rothstein goes on to
say that such an experience is by no means unique to him. He notes
that music and math have been associated
throughout history.
Pythagoras
and his followers saw numbers as models of everything in the
physical world, and they identified music
with numbers, noting its
scales, tempos, and
other regularities. Johannes Kepler envisioned planetary
motions as the "music of the
spheres." Galileo Galilei speculated
on the numerical reasons why
some combinations of tones are more pleasing than others.
Leonhard Euler considered the same problem in a treatise
on consonance and
whole numbers. Johann Sebastian Bach sometimes
treated the
composition of canons and other types of music as exercises akin to solving
mathematical puzzles. Frederic Chopin
described the fugue
as "pure logic in music." And 20th century composers have applied
sophisticated
mathematical theory in their works.
In his 1993 book,
The Music of the Spheres, music critic Jamie James examines
and ponders the history of the concept of a musical universe --
a cosmos envisioned
as a stately, ordered mechanism both mathematical and musical.
Music and science were once intimately intertwined and
united by a grand
vision, he points out. But music, like much of the most
fundamental art and literature of our culture, has now been
relegated to the
obscure margins of
the curriculum.
"All art, including
music, was a much more serious matter before the self-conscious
aestheticism of the late nineteenth century took root,"
James argues. "It is a
recent notion that music is a divertissement to be enjoyed in
comfortable surroundings at the end of the day, far
removed from
the hurly-burly of life's
business."
I was reminded of
these ideas when I read a report in the latest issue of Nature
about a study suggesting that a weekly, structured music
program can boost reading and
math skills in early elementary school. The study was done by
Martin F. Gardiner and Alan Fox of The
Music School in Providence, R.I.,
Faith Knowles of the Kodaly Center of America, and Donna Jeffrey
of the Start with Arts Program.
The study involved 96
first graders between the ages of 5 and 7 in eight public school
classrooms. Forty-eight of the students were exposed
to a weekly singing
program that emphasized the sequenced development of pitch and
rhythm, often through musical games. The second
group of 48 attended music
appreciation classes -- musical training for that age typical of
the U.S. public school curriculum. Many of the
pupils enrolled in the singing
program had performed poorly in kindergarten, compared to those in
the second, or control, group. After
7 months of the new program, however,
children in the first group had significantly improved their
attitude and behavior, caught up in
reading ability, and
outstripped the control group in
mathematics.
The researchers found
comparable results when the study continued into the second grade,
with the addition of a few new students to the
structured singing
program. Interestingly, students who had received 2 years of extra
music showed a higher level of achievement in
mathematics than those not in the
program or those in it for only 1 year.
In their report,
Gardiner and his colleagues suggest that the pupils responded to
the "pleasurable" aspects of the weekly music program,
which motivated them to
acquire the necessary skills to progress. Such training forced
mental development that was useful in other areas of learning,
particularly
mathematics.
"The maths learning
advantage in our data could, for example, reflect the development
of mental skills such as ordering and other elements
of thinking on which
mathematical learning at this age also depends," the researchers
conclude. That's not entirely
implausible. Earlier
studies by other groups had suggested links
between improved math scores and learning to play a musical instrument.
To my mind, however,
the study reported in Nature has too many loose ends to
provide satisfactory answers to the issues it was trying to
address. There really
isn't enough information to explain how this particular musical
program appeared to succeed for this particular group
of pupils. Perhaps the
pupils simply benefited from the special attention they received
from dedicated teachers who truly loved what they
were doing and conveyed this
enthusiasm to their students. Maybe it wasn't the content of the
lessons but the spirit that mattered.
Yet the intriguing
interplay between mathematics and music, which goes back to
antiquity and possibly much earlier in human history, hints
that there may be
something deeper and more basic here.
In his conclusion,
Rothstein comments that music and mathematics share not only the
clarity of their expression but also their beauty and
mystery. "Our attempt
to comprehend music and mathematics, to understand their workings
and their purposes, is . . . a model for our
coming to know at all
-- a model for our education, for the ways we make distinctions
and connections.
"We begin with
objects that look dissimilar. We compare, find patterns, analogies
with what we already know. We step back and create
abstractions,
laws, systems, using transformations, mappings, and metaphors.
This is how mathematics grows increasingly abstract
and powerful; it is
how music obtains much of its power, with grand structures growing
out of small details."
In music and
mathematics, it may be just a modest, but mind-opening, step from
the kindergarten to the cosmos.
Copyright © 1996 by
Ivars Peterson.

ARTICLE # 5
Symmetry and ASYMMETRY in ART
Excerpt
taken from an article by
Natasha Wallace on John Singer Sargent's Lady Agnew
I remember
reading an article on the nature of beauty. It was trying to
 establish
if there was some objective yardstick in which we see things as
beautiful. Their conclusions were that indeed there is an
objective establish
if there was some objective yardstick in which we see things as
beautiful. Their conclusions were that indeed there is an
objective
measure of
beauty, and it seemed to lie within the idea of symmetry. (why
symmetry?)
When I step closer to
Lady Agnew, it is apparent she is a beautiful woman with a near
perfect symmetrical face -- that is, when the face is
at rest -- "almost
schematic" is what Ratcliff calls it. But the things that I
notice, and what Ratcliff points out are the things that are
not
symmetrical and it is these things
that give her character and brings the picture to life for me --
Interesting.
Both Charteris and
Richard Ormond with Elaine Kilmurry talk in their books about the
nervous energy of the women in Sargent's portraits. Lady
Agnew is no exception
here. Although she sits with a total comfortable familiarity with
her surroundings and takes ownership of the room -- the
"languid pose", her
back to the corner of the chair, leg crossed and angled from her
left to right, there is an energy (subtle though it is)
which is palatable. Besides the mouth and
her cocked eyebrow, I notice also the hand that grips the chair,
the ever so slight downward tilt
of Lady Agnew's head (contrasted by the
hint of upward tilt to Madame X's -- although it actually doesn’t)
-- the tension here is undeniable.
The thing that
strikes me over and over about his life is that John Sargent loved
women -- women who were strong in character, intelligent
and of course beautiful
women. He didn't feel threatened by strong women (as some men
can), and above all he truly enjoyed their presence.
Yet John was not, by
anyone's measure, a wilting violet. In fact, he was a true man's
man (this comes from many sources) -- over six feet tall
and strong in physique
and sporting a full beard. His constitution was incredible and he
could push himself hard in work and he did. He
was extremely bright, well read and
seemed to retain everything he read. He was opinionated, yet
self-abasing, and his manner was charming
and humorous. He was a skilled
pianist and played often for friends and played while painting
with sitters, moving back and forth between
piano and painting. It was from music that
he seemed to draw his energy for painting and it was music that
occupied many of his sittings.
(Sargent's Musical Talents)
By: Natasha Wallace
Copyright 1998-99
Article # 6 Looking
Good: The Psychology and Biology of Beauty
Charles Feng
Human Biology, Stanford University
feng@jyi.org
In ancient
Greece, Helen of Troy, the instigator of the Trojan War, was the
paragon of beauty, exuding a physical
|
 |
|
Model Cindy Crawford,
an example of symmetry
Image courtesy of
www.cindy.com |
brilliance that would put Cindy
Crawford to shame. Indeed, she was the toast of Athens, celebrated
not for her kindness or
her intellect, but for her physical perfection. But why did the
Greek men find
Helen, and other beautiful
women, so intoxicating?
In an attempt to answer this
question, the philosophers of the day devoted a great deal of time
to
this conundrum. Plato wrote of
so-called "golden proportions," in which, amongst other things,
the
width of an ideal face would be
two-thirds its length, while a nose would be no longer than the
distance between the eyes.
Plato's golden proportions, however, haven't quite held up to the
rigors
of modern psychological
and biological research -- though there is credence in the ancient
Greeks'
attempts to determine a
fundamental symmetry that humans find attractive.
Symmetry is attractive to the
human eye
Today, this symmetry has been scientifically proven to be
inherently attractive to the human eye. It has been defined
not with
proportions, but rather with similarity between the left and right
sides of the face Thus, the Greeks were only
partially
correct.
By applying the stringent
conditions of the scientific method, researchers now believe
symmetry is the answer the
Greeks were looking for.
Babies spend more time staring
at pictures of symmetric individuals than they do at photos of
asymmetric ones.
Moreover, when several faces
are averaged to create a composite -- thus covering up the
asymmetries that any
one individual may have -- a
panel of judges deemed the composite more attractive than the
individual pictures.
Victor Johnston of New Mexico
State University, for example, utilizes a program called
FacePrints, which shows
viewers facial images of
variable attractiveness. The viewers then rate the pictures on a
beauty scale from one
to nine. In what is akin to
digital Darwinism, the pictures with the best ratings are merged
together, while the l
ess attractive photos are
weeded out. Each trial ends when a viewer deems the composite a
10. All the perfect
10s are super-symmetric.
Scientists say that the
preference for symmetry is a highly evolved trait seen in many
different animals. Female
swallows, for example,
prefer males with longer and more symmetric tails, while female
zebra finches mate with
males with symmetrically
colored leg bands.
The rationale behind symmetry
preference in both humans and animals is
that symmetric individuals have
a higher mate-value; scientists believe that
this symmetry is equated
with a strong immune system. Thus, beauty is i
ndicative of more robust genes,
improving the likelihood that an individual's
offspring will survive. This
evolutionary theory is supported by research showing
that standards of
attractiveness are similar across cultures.
According to a University of
Louisville study, when shown pictures of different
individuals, Asians, Latinos,
and whites from 13 different countries all had the
same general preferences
when rating others as attractive -- that is those that
are the most symmetric.
Beauty beyond
symmetry
However, John Manning of the University of Liverpool in England
cautions against over-generalization, especially by
Western scientists. "Darwin
thought that there were few universals of physical beauty because
there was much variance
in appearance and
preference across human groups," Manning explained in email
interview. For example, Chinese men
used to prefer women with small
feet. In Shakespearean England, ankles were the rage. In some
African tribal cultures,
men like women who insert large
discs in their lips. Indeed, "we need more
cross-cultural studies to show that what is
true in Westernized
societies is also true in traditional groups," Manning said his 1999
article.
Aside from symmetry, males in
Western cultures generally prefer females with a small jaw, a
small nose, large eyes,
and defined cheekbones -
features often described as "baby faced", that resemble an
infant's. Females, however, have
a preference for males
who look more mature -- generally heart-shaped, small-chinned
faces with full lips and fair skin.
But during menstruation,
females prefer a soft-featured male to a masculine one. Indeed,
researchers found that
female perceptions of beauty
actually change throughout the month.
When viewing profiles, both
males and females prefer a face in which the forehead and jaw are
in vertical alignment.

Altogether, the preference for
youthful and even infant-like, features, especially by
menstruating women, suggest
people with these features have
more long-term potential as mates as well as an increased level of
reproductive
fitness. Scientists have also found that
the body's proportions play an important role in perceptions of
beauty
as well. In general, men have a preference for
women with low waist-to-hip ratios (WHRs), that is, more
adipose
is deposited on the hips and buttocks than on the
waist. Research shows that women with high WHRs
(whose bodies are
more tube-shaped) are more likely to suffer from
health maladies, including infertility and diabetes. However, as
is
often the case, there are exceptions to the rule.
Psychologists at Newcastle
University in England have shown that an indigenous people located
in southeast Peru,
who have had little contact
with the Western world, actually have a preference for high WHRs.
These psychologists
assert that a general
preference for low WHRs is a byproduct of Western culture.
Beauty and choosing a
mate
Psychological research suggests
that people generally choose mates with a similar level of
attractiveness. The
evolutionary theory is that by
mating with someone who has similar genes, one's own genes are
conserved. Moreover,
a person's demeanor and
personality also influences how others perceive his or her beauty.
In one study, 70% of college
students deemed an instructor physically attractive when he acted
in a friendly manner,
while only 30% found him
attractive when he was cold and distant. Indeed, when surveyed for
attributes in selecting
a mate, both males and
females felt kindness and an exciting personality were more
important in a mate than good
looks. Thus, to a certain
degree, beauty truly is in the eye of the beholder.
Douglas Yu of the University of
East Anglia in Norwich, England, agrees. "It's true by definition.
Beauty is always
judged by the receiver," he
says. At the same time, he says in an email "there is
inter-observer concordance, a measure
of objectivity," so that
individual perceptions of beauty, factoring in other
characteristics such as personality and
intelligence, can often be
aggregated to form a consensus opinion. One of the offshoots of
Yu's work in ethnobiology
was a piece in Nature
in 1998 that showed that the hourglass-body standard of beauty in
women, previously thought
to be `universally'
preferred, was in fact likely swayed by advertising.
The halo effect
In society, attractive people tend to be more intelligent, better
adjusted, and more popular. This is described as the
halo effect - due to the
perfection associated with angels. Research shows attractive
people also have more
occupational success and more
dating experience than their unattractive counterparts. One theory
behind this halo
effect is that it is accurate
-- attractive people are indeed more successful.
An alternative explanation for
attractive people achieving more in life is that we automatically
categorize others before
having an opportunity to
evaluate their personalities, based on cultural stereotypes which
say attractive people must be
intrinsically good, and ugly
people must be inherently bad. But Elliot Aronson, a social
psychologist at Stanford University,
believes self-fulfilling
prophecies - in which a person's confident self-perception,
further perpetuated by healthy feedback
from others - may play a
role in success as well. Aronson suggests, based on the
self-fulfilling prophecy that people
who feel they are attractive -
though not necessarily rated as such - are just as successful as
their counterparts who
are judged to be good-looking.
Whatever the reason, the notion
that attractiveness correlates with success still rings true. Yet
beauty is not always
advantageous, for beautiful
people, particularly attractive women, tend to be perceived as
more materialistic, snobbish,
and vain.
  For
better or worse, the bottom line is that research shows beauty
matters; it pervades society and affects how we For
better or worse, the bottom line is that research shows beauty
matters; it pervades society and affects how we
choose loved ones. Thus,
striving to appear attractive may not be such a vain endeavor
after all. This isn't to say
plastic surgery is necessarily
the answer. Instead, lead a healthy lifestyle that will in turn
make you a happier person.
|